Serie de Fourier
Una serie de Fourier es una serie infinita que converge puntualmente a una función periódica y continua a trozos (o por partes). Las series de Fourier constituyen la herramienta matemática básica del análisis de Fourier empleado para analizar funciones periódicas a través de la descomposición de dicha función en una suma infinita de funciones sinusoidales mucho más simples (como combinación de senos y cosenos con frecuencias enteras). El nombre se debe al matemático francés Jean-Baptiste Joseph Fourier, que desarrolló la teoría cuando estudiaba la ecuación del calor. Fue el primero que estudió tales series sistemáticamente, y publicó sus resultados iniciales en 1807 y 1811. Esta área de investigación se llama algunas veces análisis armónico.
Es una aplicación usada en muchas ramas de la ingeniería, además de ser una herramienta sumamente útil en la teoría matemática abstracta. Áreas de aplicación incluyen análisis vibratorio, acústica, óptica, procesamiento de imágenes y señales, y compresión de datos. En ingeniería, para el caso de los sistemas de telecomunicaciones, y a través del uso de los componentes espectrales de frecuencia de una señal dada, se puede optimizar el diseño de un sistema para la señal portadora del mismo. Refiérase al uso de un analizador de espectros.
Las series de Fourier tienen la forma:
Donde
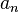 y
y  se denominan coeficientes de Fourier de la serie de Fourier de la función
se denominan coeficientes de Fourier de la serie de Fourier de la función 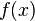
Definición
Si 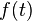 es una función (o señal) periódica y su período es
es una función (o señal) periódica y su período es  , la serie de Fourier asociada a
, la serie de Fourier asociada a 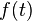 es:
es:
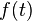 es una función (o señal) periódica y su período es
es una función (o señal) periódica y su período es  , la serie de Fourier asociada a
, la serie de Fourier asociada a 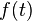 es:
es:
Donde  ,
,  y
y  son los coeficientes de Fourier que toman los valores:
son los coeficientes de Fourier que toman los valores:
 ,
,  y
y  son los coeficientes de Fourier que toman los valores:
son los coeficientes de Fourier que toman los valores:
Por la identidad de Euler, las fórmulas de arriba pueden expresarse también en su forma compleja:
Los coeficientes ahora serían:
Otra forma de definir la serie de Fourier es:
donde 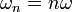 y
y 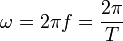
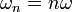 y
y 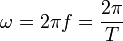
siendo:
a esta forma de la serie de Fourier se le conoce como la serie trigonométrica de Fourier.
Forma compacta
En ocasiones es más útil conocer la amplitud y la fase en términos cosinusoidales en lugar de amplitudes cosinusoidales y sinusoidal. Otra forma de expresar la compleja forma de la serie de Fourier es:
donde
Forma exponencial
Por la identidad de Euler para la exponencial compleja, operando adecuadamente, si
la serie de Fourier se puede expresar como la suma de dos series:
En forma más compacta:
estas ecuaciones solo son válidas cuando el periodo  con
con 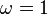 . Otra forma de expresar la forma compleja de la serie de Fourier es:
. Otra forma de expresar la forma compleja de la serie de Fourier es:
 con
con 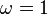 . Otra forma de expresar la forma compleja de la serie de Fourier es:
. Otra forma de expresar la forma compleja de la serie de Fourier es:
donde
Formulación moderna
Realmente el desarrollo en serie de Fourier se hace para funciones de cuadrado integrable, es decir, para funciones que cumplan que:
El conjunto de todas las funciones integrables definidas en el intervalo ![\scriptstyle [-\pi, \pi]](https://upload.wikimedia.org/math/c/9/5/c957ace0731ed3996ddc66f4e5cd3001.png) se denota con
se denota con ![\scriptstyle L^2([-\pi, \pi])](https://upload.wikimedia.org/math/7/5/1/7516696a518a1f5eeafa8b25b30f4168.png) . Este conjunto, tiene definido un producto interno dado por:
. Este conjunto, tiene definido un producto interno dado por:
![\scriptstyle [-\pi, \pi]](https://upload.wikimedia.org/math/c/9/5/c957ace0731ed3996ddc66f4e5cd3001.png) se denota con
se denota con ![\scriptstyle L^2([-\pi, \pi])](https://upload.wikimedia.org/math/7/5/1/7516696a518a1f5eeafa8b25b30f4168.png) . Este conjunto, tiene definido un producto interno dado por:
. Este conjunto, tiene definido un producto interno dado por:
que lo dota de estructura de espacio de Hilbert. De este modo, todas las funciones de ![\scriptstyle L^2([-\pi, \pi])](https://upload.wikimedia.org/math/7/5/1/7516696a518a1f5eeafa8b25b30f4168.png) pueden desarrollarse en series de Fourier. Así,el conjunto
pueden desarrollarse en series de Fourier. Así,el conjunto  es una base ortonormal del espacio
es una base ortonormal del espacio ![\scriptstyle L^2([-\pi,\pi])](https://upload.wikimedia.org/math/7/5/1/7516696a518a1f5eeafa8b25b30f4168.png) . El desarrollo de Fourier se puede expresar como:
. El desarrollo de Fourier se puede expresar como:
![\scriptstyle L^2([-\pi, \pi])](https://upload.wikimedia.org/math/7/5/1/7516696a518a1f5eeafa8b25b30f4168.png) pueden desarrollarse en series de Fourier. Así,el conjunto
pueden desarrollarse en series de Fourier. Así,el conjunto  es una base ortonormal del espacio
es una base ortonormal del espacio ![\scriptstyle L^2([-\pi,\pi])](https://upload.wikimedia.org/math/7/5/1/7516696a518a1f5eeafa8b25b30f4168.png) . El desarrollo de Fourier se puede expresar como:
. El desarrollo de Fourier se puede expresar como:
Donde 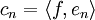 son los coeficientes del desarrollo de Fourier.
son los coeficientes del desarrollo de Fourier.
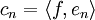 son los coeficientes del desarrollo de Fourier.
son los coeficientes del desarrollo de Fourier.
Por último, la identidad de Parseval dice que dada una función  de cuadrado integrable y los coeficientes de Fourier
de cuadrado integrable y los coeficientes de Fourier  , se verifica que:
, se verifica que:
 de cuadrado integrable y los coeficientes de Fourier
de cuadrado integrable y los coeficientes de Fourier  , se verifica que:
, se verifica que:
En lenguaje técnico, podríamos decir que hay una isometría entre el espacio de funciones de cuadrado integrable y el espacio de sucesiones lineales indexadas en los enteros cuyos términos tienen cuadrados sumables.
Formulación general
Las propiedades útiles de las series de Fourier se deben principalmente a la ortogonalidad y a la propiedad de homomorfismo de las funciones ei n x.
Otras sucesiones de funciones ortogonales tienen propiedades similares, aunque algunas identidades útiles, concerniendo por ejemplo a las convoluciones, no seguirán cumpliéndose si se pierde la "propiedad de homomorfismo".
Algunos ejemplos son las secuencias de funciones de Bessel y los polinomios ortogonales. Tales sucesiones se obtienen normalmente como soluciones de una ecuación diferencial; una gran clase de tales sucesiones útiles son soluciones de los llamados problemas de Sturm-Liouville.
Aplicaciones
- Generación de formas de onda de corriente o tensión eléctrica por medio de la superposición de sinusoides generados por osciladores electrónicos de amplitud variable cuyas frecuencias ya están determinadas.
- Análisis en el comportamiento armónico de una señal.
- Reforzamiento de señales.
- Estudio de la respuesta en el tiempo de una variable circuital eléctrica donde la señal de entrada no es sinusoidal o cosinusoidal, mediante el uso de transformadas de Laplace y/o solución en régimen permanente sinusoidal en el dominio de la frecuencia.
- La resolución de algunas ecuaciones diferenciales en derivadas parciales admiten soluciones particulares en forma de series de Fourier fácilmente computables, y que obtener soluciones prácticas, en la teoría de la transmisión del calor, la teoría de placas, etc.
Br. Gustavo Ludewig Escuela 80 Electrónica
transformada de Laplace
La transformada de Laplace es un tipo de transformada integral frecuentemente usada para la resolución de ecuaciones diferenciales ordinarias. La transformada de Laplace de una función f(t) definida (en ecuaciones diferenciales, en análisis matemático o en análisis funcional) para todos los números positivost ≥ 0, es la función F(s), definida por:
siempre y cuando la integral esté definida. Cuando f(t) no es una función, sino una distribución con una singularidad en 0, la definición es
Cuando se habla de la transformada de Laplace, generalmente se refiere a la versión unilateral. También existe la transformada de Laplace bilateral, que se define como sigue:
La transformada de Laplace F(s) típicamente existe para todos los números reales s > a, donde a es una constante que depende del comportamiento de crecimiento de f(t).
 es llamado el operador de la transformada de Laplace.
es llamado el operador de la transformada de Laplace.Linealidad
Derivación
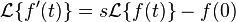 .
.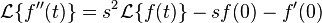
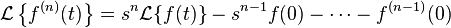
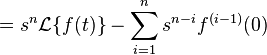
Integración
Dualidad
Desplazamiento de la frecuencia
Desplazamiento temporal
Nota:  es la función escalón unitario.
es la función escalón unitario.
 es la función escalón unitario.
es la función escalón unitario.Desplazamiento potencia n-ésima
Convolución
Transformada de Laplace de una función con periodo p
Condiciones de convergencia
 (que crece más rápido que
(que crece más rápido que  ) no pueden ser obtenidas por Laplace, ya que
) no pueden ser obtenidas por Laplace, ya que 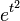 , es una función de orden exponencial de ángulos.
, es una función de orden exponencial de ángulos.
Teorema del valor inicial
Sea una función 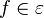 derivable a trozos y que
derivable a trozos y que 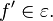 Entonces :
Entonces :
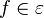 derivable a trozos y que
derivable a trozos y que 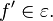 Entonces :
Entonces :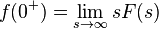
 es el conjunto de funciones continuas a trozos con orden exponencial.
es el conjunto de funciones continuas a trozos con orden exponencial.Teorema del valor final
Sea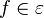 una función derivable a trozos tal que
una función derivable a trozos tal que  .Entonces :
.Entonces :
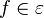 una función derivable a trozos tal que
una función derivable a trozos tal que  .Entonces :
.Entonces :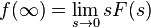
 es el conjunto de funciones continuas a trozos con orden exponencial.
es el conjunto de funciones continuas a trozos con orden exponencial.
Relación con otras transformadas
La transformada de Laplace está estrechamente relacionada con la Transformada de Fourier y la Transformada Z.
Br. Elisa Pizano Escuela 80 Electrónica
Transformada Z
El nombre de Transformada Z procede de la variable del dominio, al igual que se podría llamar "Transformada S" a la Transformada de Laplace. Un nombre más adecuado para la TZ podría haber sido "Transformada de Laurent", ya que está basada en la serie de Laurent. La TZ es a las señales de tiempo discreto lo mismo que Laplace a las señales de tiempo continuo.
La transformada Z, al igual que otras transformaciones integrales, puede ser definida como una transformada unilateral o bilateral.
Transformada Z bilateral
La TZ bilateral de una señal definida en el dominio del tiempo discreto x[n] es una función X(z) que se define
donde n es un entero y z es, en general, un número complejo de la forma
donde A es el módulo de z, y ω es el argumento de ese complejo que bien podría representar la frecuencia angular (pulsación) en radianes por segundo (rad/s).
Transformada Z unilateral
De forma alternativa, en los casos en que x[n] está definida únicamente para n ≥ 0, la transformada Z unilateral se define como
En el procesamiento de señales, se usa esta definición cuando la señal es causal. En este caso, la Transformada Z resulta una serie de Laurent, con ROC del tipo  ; es decir que converge "hacia afuera".
; es decir que converge "hacia afuera".
 ; es decir que converge "hacia afuera".
; es decir que converge "hacia afuera".
Un ejemplo interesante de la TZ unilateral es la función de generación de probabilidades, donde x[n] es la probabilidad que toma una variable discreta aleatoria en el instante n, y la función X(z) suele escribirse como X(s), ya que s = z−1. Las propiedades de las transformadas Z son útiles en la teoría de la probabilidad.
Br. Víctor Mejías Escuela 80 Electrónica
![\frac{a_0}{2} + \sum_{n=1}^\infty\left[a_n\cos\frac{2n\pi}{T}t + b_n\sin\frac{2n\pi}{T}t\right]](https://upload.wikimedia.org/math/5/5/8/558025a943d5a46c353605d33c6b6d2c.png)
![f(t) \sim \frac{a_0}{2} + \sum_{n=1}^\infty\left[a_n\cos \left( \frac{2n\pi}{T}t \right) + b_n\sin \left( \frac{2n\pi}{T}t \right) \right]](https://upload.wikimedia.org/math/4/2/4/424e2257d1e18bf4fb095a66f77d6aba.png)
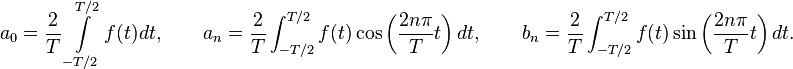

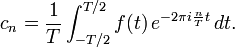
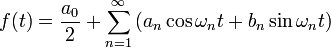
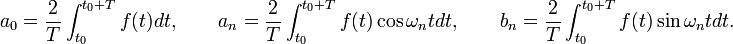
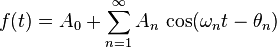
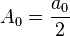


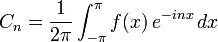

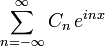
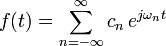
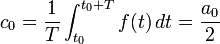

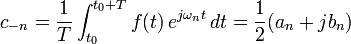
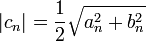
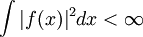
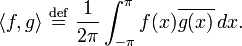
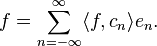

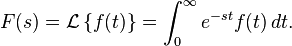



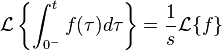
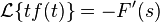
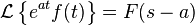
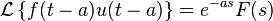
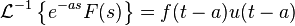
![\mathcal{L}\{\,t^nf(t)\} = (-1)^nD_s^n[F(s)]](https://upload.wikimedia.org/math/f/7/5/f75194212391d819688d6d298bd219d0.png)
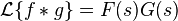
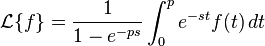
![X(z) = Z\{x[n]\} = \sum_{n=-\infty}^{\infty} x[n] z^{-n} \](https://upload.wikimedia.org/math/7/d/d/7dd277c71c1256a3437490679567cfba.png)
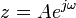
![X^{+}(z) = Z^{+}\{x[n]\} = \sum_{n=0}^{\infty} x[n] z^{-n} \](https://upload.wikimedia.org/math/e/2/a/e2a99fb60f5b075b50d3fb6db7472c9a.png)